基于网格空间分解的GPU加速多代理路径规划

Giuseppe Caggianese, Ugo Erra

Dipartimento di Matematica e Informatica, Universit`a della Basilicata, Viale Dell’Ateneo, Macchia Romana, 85100, Potenza, Italy

原文链接

Abstract

​ 在这项工作中，我们描述了一种简单而强大的方法来在图形处理器单元（GPU）上实现实时多代理寻路。 该技术旨在使用 A* 算法和划分为块的输入网格图，为数千个代理找到潜在路径。 我们提出了一种 GPU 实现，它使用搜索空间分解方法将前向搜索 A* 算法分解为并行独立的前向子搜索。 我们证明这种方法非常适合 GPU 的编程模型，可以在计算机游戏和机器人等实时应用程序中并行规划数千个代理。 该论文使用统一计算设备架构编程环境描述了该实现，并展示了与实时自适应 A* 的 GPU 实现相比，其在 GPU 性能方面的优势。

1.Introduction

​ 多代理的导航规划技术传统上在机器人领域进行研究，近年来越来越多地应用于实时策略游戏和视频游戏中的非玩家角色。在这些应用中，主要的挑战是安全性 将代理导航至目标位置，同时避免与静态或动态障碍物以及其他移动代理发生碰撞。 因此，代理不是由人类直接控制，而是依赖于路径规划算法。A*[1] 是最著名的在状态空间中查找成本最小路径的算法，通常表示为图。 给定起始状态（或起始节点）和目标状态（或目标节点），A* 通过使用距离成本启发式函数确定搜索访问状态的顺序来找到成本最小的路径。 A* 执行的搜索非常适合离线人工智能应用，对于每个代理，我们依次执行从起始状态到目标状态的搜索。 然而，它不适合实时搜索路径，其中图的拓扑、其边缘成本、起始状态或目标状态随时间变化。 人们已经开发了几种方法来解决这些问题，例如Fringe Saving A*, Generalized Adaptive A*, Lifelong Planning A*, and D*。 本文值得注意的是实时自适应 A(RTAA*) [2]，我们将其用作性能基准测试的比较。

​ 在代理导航到其目标位置以避免碰撞的场景中，例如使用 A*，对数千个代理的规划非常适合并行计算数据范例。 本质上，对于每个代理，单个程序 A* 会查阅全局连接数据，并同时解析代理的最佳路径，该路径受起始位置和目标位置的约束。 随着代理数量和搜索空间大小的增加，规划往往会变得计算繁重。 因此，大地图上的寻路可能会导致严重的性能瓶颈。 在过去几年中，图形处理器单元 (GPU) 迅速普及，因为它们提供了加速许多算法的机会。 特别是，具有大量并行线程的应用程序在同步有限的情况下跨多个数据点执行类似的工作，是利用 GPU 加速的良好候选者。 所有这些意味着，在具有大型地图的多代理场景中，我们可以考虑这样的想法：不同路径的探索可以与探索同时子路径的大量线程并行执行。 这些子路径可能会在不同代理的路径之间共享。

​ 在本文中，我们描述了一种使用 A* 的数千个代理的路径规划系统的方法。该方法基于输入网格图的搜索空间分解为块。 对于所有块，我们同时执行 A* 搜索，以获得输入代理朝向遍历这些块的目标状态的所有潜在子路径。 通过这种方式，给定代理的起始位置和目标位置作为输入，我们能够将前向搜索 A* 算法分解为并行独立的前向子搜索。 这种方法非常适合 GPU 的并行架构，其中需要数百个线程才能充分利用 GPU。此外，我们的方法简单且易于使用 GPU 编程模型（例如本工作中选择的平台，NVIDIA 的平台）来实现。 计算统一设备架构 (CUDA)。 实证结果表明，与 RTAA* 和次优解决方案的 GPU 实现相比，大量代理的 GPU 性能加速优势，从而以最优性换取更高的执行性能。 这提供了一种强大的方法来加速实时应用程序（例如机器人和计算机游戏）中的同步路径规划。

​ 本文的其余部分组织如下。 第 2 节涉及并行路径规划问题的类似工作。 第 3 节正式介绍了 A* 算法并简要说明了 GPU 编程模型。 第 4 节描述了我们的并行路径规划方法的基础知识。 在第 5 节中，我们将介绍有关 GPU 上实现的一些细节。 在第 6 节中，我们评估性能权衡和质量结果。 最后，在第七节中，我们提出了我们的结论和未来的研究方向。

2.Related Work

​ 研究人员最近开发了基于并行的寻路实现，利用 GPU 的计算能力。 2008 年，Bleiweiss [3] 使用 CUDA 实现了 Dijkstra 和 A* 算法。 经过几次基准测试后，他观察到 Dijkstra 实现的速度比传统方法提高了 27 倍。
不使用 SSE 指令的 C++ 实现，而与使用 SSE 指令的 C++ 实现相比，A* 实现的速度提高了 24 倍。 在[4]中，卡茨等人。 提出了所有对最短路径问题的高速缓存高效 GPU 实现，并证明它可以显着提高性能。 在[5]中，Stefan 等人。 使用 GPU 上搜索前沿的位向量表示获得了广度优先搜索的加速。 在[6]中，Kider 等人。 提出了一种随机启发式搜索的新颖实现，即 R* 搜索，可扩展到更高维的规划问题。 他们演示了如何在 GPU 上实现 R*，并表明它能够始终如一地生成更低成本的解决方案，在内存方面具有更好的扩展性，并且在中央处理单元 (CPU) 上比 R* 运行得更快。 在[7]中，Erra 等人。 提出一种基于 RTAA* 算法的高效 GPU 多代理规划方法。 RTAA* 的实施可以通过每个代理使用有限的内存占用来规划数千个代理。 此外，与运行一、二和四线程的多线程 CPU 实现相比，基准测试支持 GPU CUDA 性能规模。

​ 这些方法提供了强有力的证据，证明 GPU 可以大幅加速寻路算法，特别是对于视频游戏和机器人实时应用等实时应用，这些应用需要高效的寻路来支持大量代理在广阔且日益增长的大型动态环境。

3.Background

在本节中，我们向读者介绍 A* 算法和 GPU 编程模型。

3.3. A* Algorithm

​ 在解释所提出的方法之前，我们先简要概述一下 A*。 在 A*（算法 1）中，对于每个状态 s，用户提供一个启发式 h[s] 来估计目标距离，即从状态 s 到目标状态的最小路径的成本。 经典启发法基于曼哈顿距离、对角线距离或欧几里得距离计算。 在执行过程中，A* 维护两个值：g[s] 和 f[s]。 值 g[s] 是从起始状态 sstart 到状态 s 的任何已发现路径的最小成本。 值 f[s] = g[s]+h[s] 估计从 sstart 通过状态 s 到目标状态的距离。 该算法维护两个列表：打开列表和关闭列表。 打开列表是一个优先级队列，包含最近发现的状态。 最初它仅包含启动状态 sstart。 关闭列表包含扩展状态，其中所有相邻状态都已被探索并插入到打开列表中。 在每次迭代中，A* 从打开列表中删除具有最小 f[s] 值的状态 s。 如果状态 s 是目标状态，则终止。 否则，它会探索相邻状态并更新每个访问状态的 g 值。 如果 g 值减小，则会更新 open 列表中的 g 值和相应的 f 值。 然后它会重复这个过程。 最后，每个访问过的状态 s 的 g 值将是从起始状态 s_start 到状态 s 的距离。

image-20240414204007271

​ 对于实时应用程序，A* 有两个主要缺点。 第一个是执行从起始状态到目标状态的搜索所需的计算时间。 第二个缺点与算法执行期间的内存占用有关。 每个代理必须存储并更新每个状态 s 的 h[s]、g[s] 和 f[s] 值。 这使得 A* 不适合在内存有限的情况下在大状态空间中进行多代理路径规划。

3.2. The GPU programming model

​ 在过去几年中，GPU 性能的提高促使研究人员探索将通用非图形计算映射到这些新的并行架构上。 GPGPU 现象已经显示出一些令人印象深刻的结果，但通过图形 API 映射问题的局限性和困难使得这些成功的实验只能由 3D 图形专家进行。 使用 GPU 作为更通用的并行处理器的需求促使 NVIDIA 在 2006 年发布了新一代显卡（所谓的 G80 架构或其后继者之一），通过新的统一图形和计算，显着将 GPU 扩展到图形之外。 GPU 架构和 CUDA 编程模型 [8]。

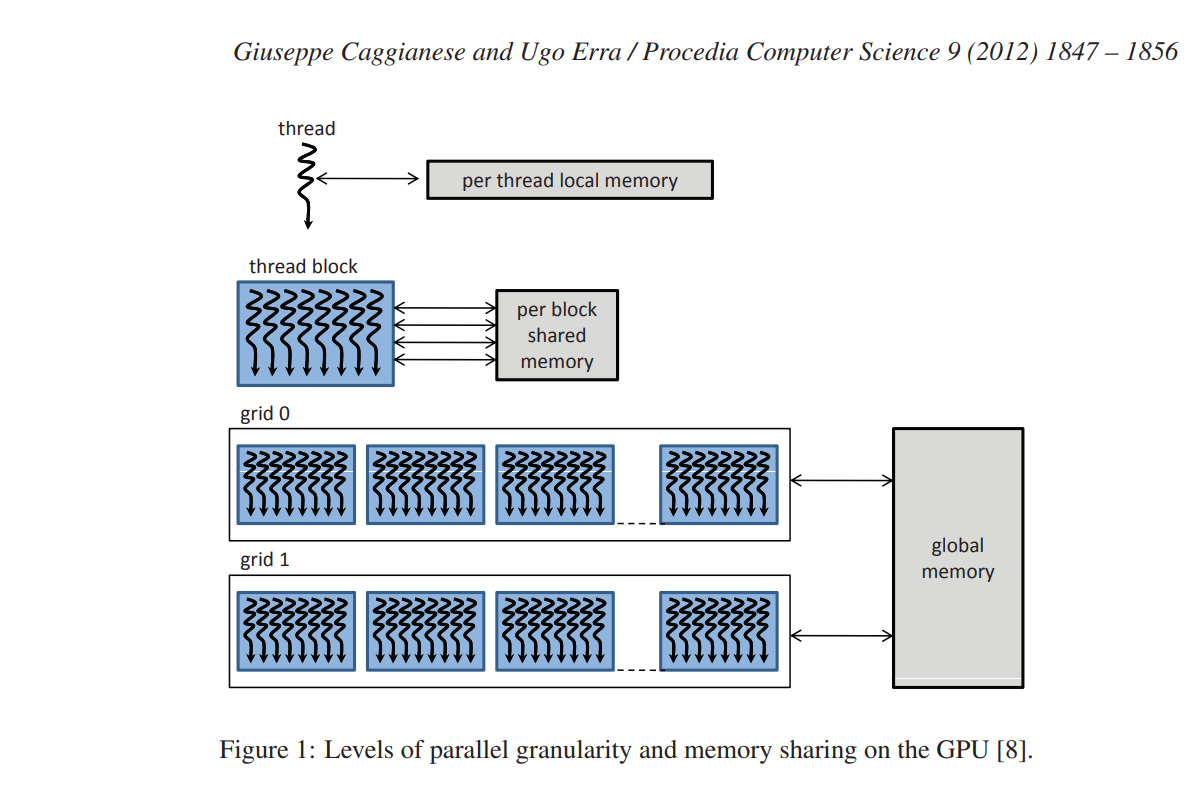
image-20240414204255026

​ 从硬件模型的角度来看，GPU架构被构建为可扩展的多线程多处理器阵列。 每个多处理器由许多 SIMD ALU 组成，称为处理器。 处理器同时以 SIMD 方式执行相同的指令，并可以访问本地寄存器。 在多处理器级别，多处理器的所有处理器都可以对共享内存进行读/写访问。

​ 从软件模型的角度来看，CUDA是C语言的最小扩展，它允许编写称为内核的串行程序。 内核通过一组并行线程并行执行。 按照图 1 中的表示，每个线程都有一个私有本地内存。 程序员将这些线程组织成线程块和网格的层次结构。 线程块是一组并发线程，它们可以通过屏障同步相互协作，并且可以以与寄存器相当的延迟访问共享内存。 网格是一组线程块，每个线程块可以独立执行。 所有线程都可以访问相同的全局、常量或纹理内存。 这三个内存空间针对不同的内存使用情况进行了优化，因此具有不同的访问时间。 例如，只读常量缓存和纹理缓存由所有标量处理器核心共享，这加快了从纹理内存空间和常量内存空间的读取速度。

​ 必须为每个内核调用定义网格和块大小。 每个块映射到一个多处理器，然后多个线程块可以映射到同一个多处理器上并并发执行。 多处理器资源（寄存器和共享内存）在映射的线程块之间分配。 因此，这限制了可以映射到同一多处理器上的线程块的数量。 为了最大化多处理器支持的线程数量，重要的是要考虑每个内核所需的资源。然后，选择使用多个内核来设计框架是利用 GPU 资源和 最大化线程并行度。

​ 有关 GPU 架构和 CUDA 编程模型的更多详细信息，请参阅 NVIDIA 的 CUDA 编程指南 [9]。

4. The Proposed Approach(提议的方法)

​ 在本节中，我们描述了一种在多代理场景中并行计算同时路径规划的方法。 作为输入，我们有一组开始状态、一个目标状态和一个代表代理移动环境的搜索空间。 我们首先描述路径规划的参考场景以及如何分解搜索空间。 然后，我们描述执行从起始状态到目标状态的并行搜索的必要步骤。

4.1. Search space decomposition(搜索空间分解)

​ 我们提出的方法适用于基于网格地图的场景。 在这些场景中，环境被细分为称为图块的小规则区域。 每个图块代表搜索空间的一个状态 s 并连接到所有附近的图块。 从一个图块移动到它的每个邻居的成本由一个整数指定。 这可用于

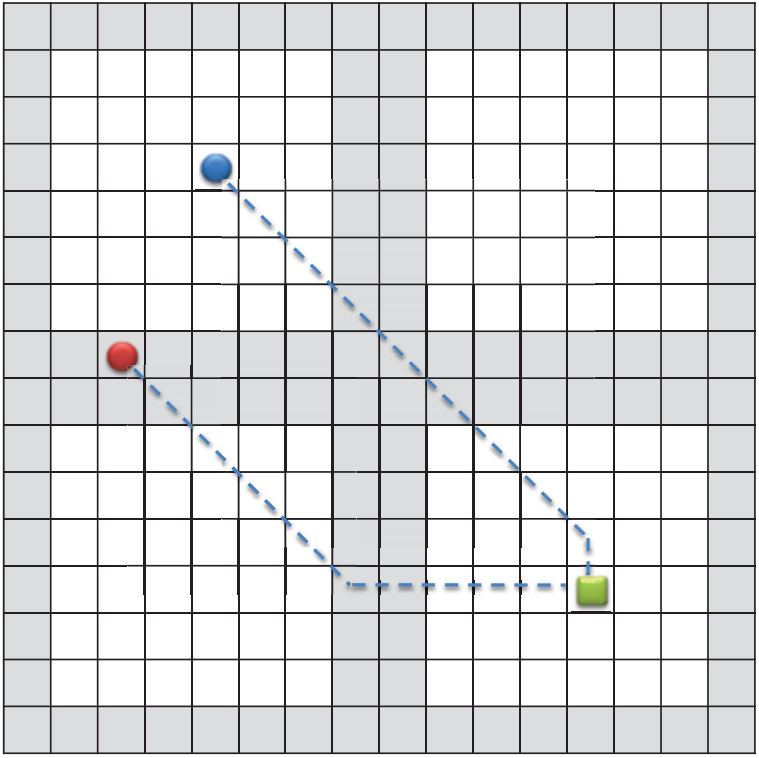
image-20240414205214985

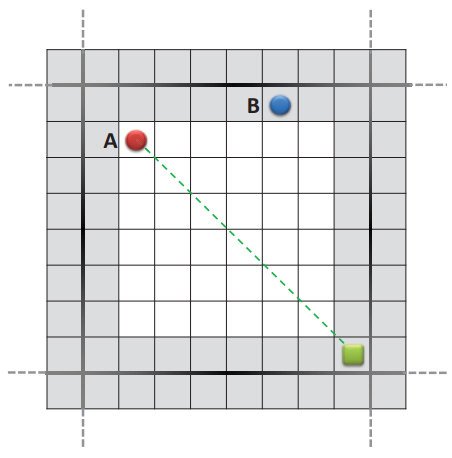
图 2：包含四个 8 × 8 规划区块的 16 × 16 网格地图示例。 灰色表示边框瓷砖。 圆圈是处于起始位置的两名代理。 正方形是目标位置，虚线是穿过规划区块的路径。

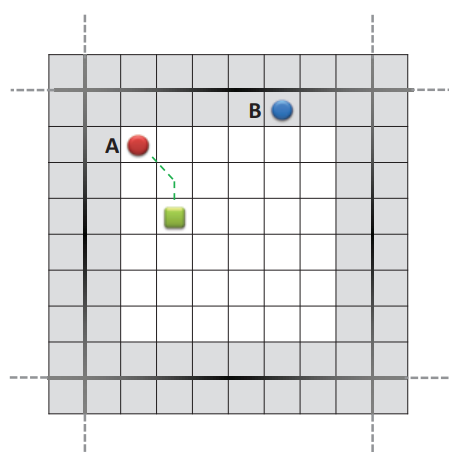
image-20240414205400756image-20240414205423615image-20240414205439841image-20240414205453963
(a) 遍历子路径。(b) 传入子路径。(c) 传出子路径。(d) 内部子路径。

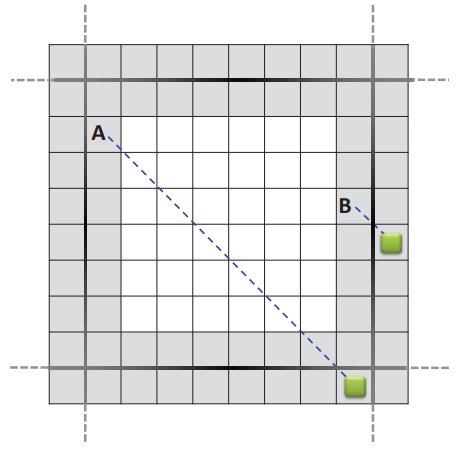
图 3：左 (a–b)：边界到边界步骤。 所有同时进行的 A* 搜索都从边界图块开始，并在相邻规划块的边界图块或目标状态中终止。 右 (c–d)：从开始到边界的步骤。 同时的 A* 搜索从代理的位置开始，并在同一规划块或目标状态的边界图块上终止。

对难以或不可能通过的地形元素进行建模，例如山丘和湖泊。 我们在这项工作中采用的用于测量网格地图上距离的常用度量是曼哈顿距离。

​ 用作搜索空间S的网格地图被进一步划分为k个规则区域Bi，称为规划块。 规划块的大小均相同，并将搜索空间分解为不重叠的搜索子空间，使得 S = B1 ∪ B2 ∪ ... ∪ Bk。 我们将规划块的边缘状态称为边界图块，它可以实现从规划块到相邻块的状态转换，如图 2 所示。

​ 给定两个不同的规划块 Bi 和 Bj，令 pi = s1, s2,..., sm 为一条子路径，其中 si ∈ Bi 对于 i = 1,..., m − 1。我们将 pi 命名为 Bi 的遍历子路径 如果 s1, sm ∈ Bj 是边界瓦片（图 3a）。 如果 sm ∈ Bi 并且 s1 是边界图块，我们将 pi 称为 Bi 的传入子路径（图 3b）。 如果 sm ∈ Bi 是边界图块，我们将 pi 称为 Bi 的传出子路径（图 3c）。 最后，如果 sm ∈ Bi 并且 si 都不是边界图块，则 pi 是 Bi 的内部子路径（图 3d）。 从起始状态到目标状态的路径 p 具有后续子路径 pi，其中 i = 1, 2,..., n。 如果n = 1，我们只有一个内部子路径。当n ≥ 3时，p1是传出子路径，p2，p3，...，pn−1是遍历子路径，pn是传入子路径。

​ 规划块背后的基本原理是分解单个路径的搜索，独立计算其所有子路径。 通过对所有规划块使用同时 A* 搜索，我们并行计算所有潜在的子路径。由于规划块的依赖性，这可能会带来问题。 在 A* 搜索期间，顺序发现路径，并且如果规划块 Bi−1 内的子路径 pi−1 然后先于规划块 Bi 内的子路径 pi，我们无法同时启动 Bi−1 和 Bi−1 的 A* 搜索 双。 然而，在多代理场景中，很自然地期望代理之间共享路径的一部分。 因此，我们可以利用这种情况，并行计算所有可能能够遍历所有规划块的子路径。

4.2. The parallel search(并行搜索)

​ 为了并行搜索数千个代理，我们需要找到一种同时使用所有规划块的方法。 我们的解决方案利用了这样一个事实：给定一组起始状态和一个目标状态，发现的路径很可能共享子路径。 我们尝试确定这些共享子路径，并行计算规划块内的所有潜在子路径类型，并考虑到它们必须向目标方向收敛。 该策略通过两个步骤实现：边界到边界搜索和开始到边界搜索。

​ 在边界到边界步骤(border-to-border step)（图 3a-b）中，我们使用多个 A* 搜索计算所有规划块的遍历子路径和传入子路径。 特别是，对于给定的规划块，A* 搜索将边界图块作为开始状态，并且搜索确定沿通往目标位置的所有状态。 当发现属于相邻规划块的边界图块或当搜索发现目标位置时，单个 A* 搜索终止。 在此步骤结束时，我们可以组装一条从任何边界图块到目标位置的路径，组装零个或多个遍历路径和传入路径的序列。 请注意，此步骤独立于起始位置，并且如果预计目标不会移动到任何地方，则可以离线执行。

​ 在开始到边界步骤（图 3c-d）中，我们使用多个 A* 搜索来计算传出子路径和内部子路径。 在这种情况下，对于所有输入代理，A*搜索将所有代理的开始位置作为开始状态，并且如上所述，搜索确定朝向目标位置的沿途的所有状态。 当发现属于同一规划块的边界图块或当搜索发现目标位置时，单个 A* 搜索终止。 因此，此步骤的目标是搜索所有代理从其起始位置到最近的边界块的路径。

​ 这种方法的优点是它可以很容易地并行实现，因为边界到边界步骤和开始到边界步骤中的所有搜索可以同时执行。 考虑到规划块内所有可能的子路径，我们消除了规划块之间的依赖性。 此外，使用小搜索区域的能力可确保更快的搜索并限制内存使用。 最后，在起始位置发生变化的情况下，我们只需要在发生变化的地方执行从开始到边界的搜索。

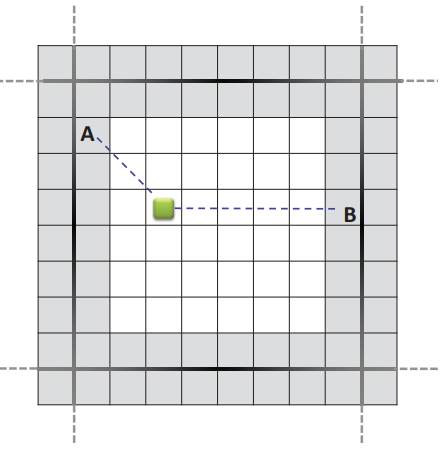
​ 与此方法相关的一个问题是在边界到边界步骤结束时形成循环，如图 4 所示。有两种可能的策略来解决此问题。 第一个是在代理移动期间处理环路，例如，防止代理被困在环路中。 第二个是增加与形成循环的边界图块相关联的启发式，然后仅针对所涉及的规划块执行新的边界到边界步骤。 这样，这些边界块将不会在新路径中被考虑，因为它们的移动成本较高。

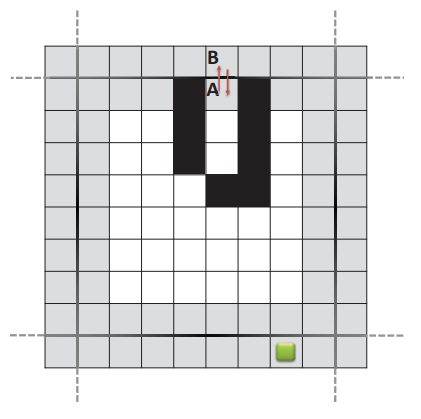
image-20240414211015612

图 4：死胡同导致从边框图块 A 进行的 A* 搜索在边框图块 B 中停止。相反，从边框图块 B 进行的 A* 搜索在边框图块中停止

5. GPU Implementation(GPU实现)

​ 在 GPU 编程模型上实现上述方法非常简单。 为了同时执行所有搜索，我们将单个 GPU 线程与每个搜索相关联； 事实上，每次搜索都执行相同的指令，但使用不同的数据。 在边界到边界步骤中，我们为每个规划块耦合一个线程块，如图 5 所示。这一决定使我们能够同时执行所有边界到边界搜索并通过共享内存共享信息。 事实上，用于估计每个状态 s 的目标距离的启发式值 h[s] 作为规划块作为单个数组存储在大型共享内存中。 这是可能的，因为在边界到边界步骤中，所有搜索都是本地的，即搜索在同一规划块中开始和停止。

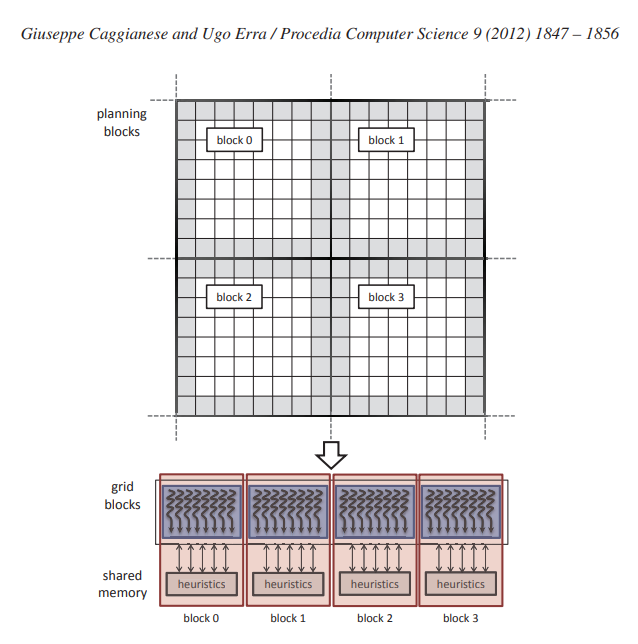
image-20240414211337457

图 5：使用 GPU 并行化边界到边界步骤。 规划块与线程块相关联，线程对每个边界图块执行搜索。 这种映射使我们能够使用线程块中的共享内存来存储规划块的估计启发式。 最后，所有规划块都聚集在一个 CUDA 网格中。

​ 相反，在开始到边界步骤(start-to-border step)中，代理的起始位置并不都位于同一规划块中。但是，即使在这种情况下，启发值数组也可以在代理之间共享。 事实上，该数组可能会变得与整个映射一样大，并且必须将其存储在全局内存中，因为其维度对于共享内存而言太大。 对于这两种类型的步骤，所有代理之间共享并存储在全局存储器中的另一个元素是地图，该地图保留从每个图块到其邻居的移动成本，因此也保留障碍物的位置。

​ 规划块大小会影响搜索的行为，因为它决定单个规划块中的状态数量、用于维护启发式的共享内存的数组维度以及边界图块的数量。如果规划块太大， A*算法需要探索的状态太多，如果太小，则在相同的时间内探索的状态较少，但要执行的搜索较多。 然而，为了优化时间执行，我们选择规划块大小始终为 2 的幂，以便我们可以使用 CUDA 按位运算来替代整数除法和模运算，这些运算的运行成本太高，并且对于检索图块坐标是必需的 以及规划块 ID。

6. Experiments and Results(实验与结果)

​ 在本节中，我们提供两个实验的结果。 第一种类型的实验证明了我们方法的效率，而第二种实验则与使用搜索空间分解找到的轨迹的质量有关。我们的测试是在 Intel Core i7 CPU 1.6GHz、NVIDIA Fermi GTX 480 1.5GB、 Windows 7。所有内核均采用 CUDA 4.0 编写并使用 Microsoft 的 Visual C++ 2010 编译器。

​ 第一个实验将我们基于规划块 (P-BA*) 的 GPU 并行方法与 RTAA* (P-RTAA*) 的 GPU 实现进行比较 [2]。 RTAA* 是一种实时启发式搜索方法，它以非常细粒度的方式选择其本地搜索空间。 其基本原理是快速更新本地搜索空间中所有状态的启发式并保存启发式以加速未来的A*搜索。 这种方法使用一个名为 Lookahead 的变量，它指定 A* 搜索期间要扩展的最大状态数，并在 GPU 实现中用于减少每个代理所需的内存占用。 我们选择将我们的方法与 RTAA* 的 GPU 并行版本进行比较，因为在之前的工作 [7] 中发现该实现比 A* [3] 的并行 GPU 实现更快。

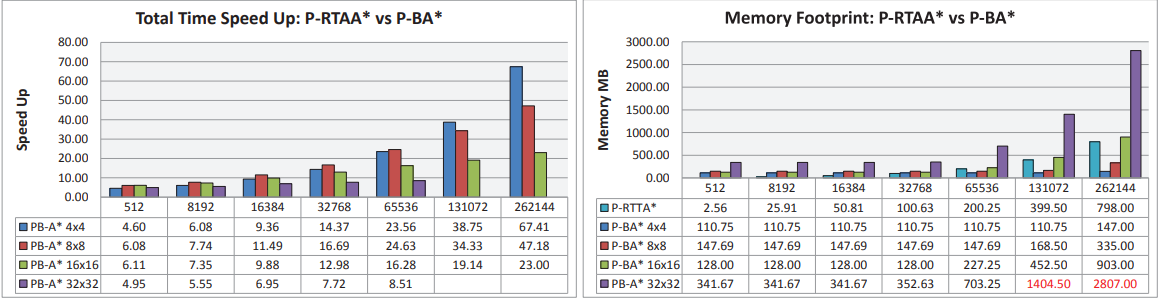image-20240414212026143
(a) 512 × 512 地图的 GPU 总时间加速和内存占用。
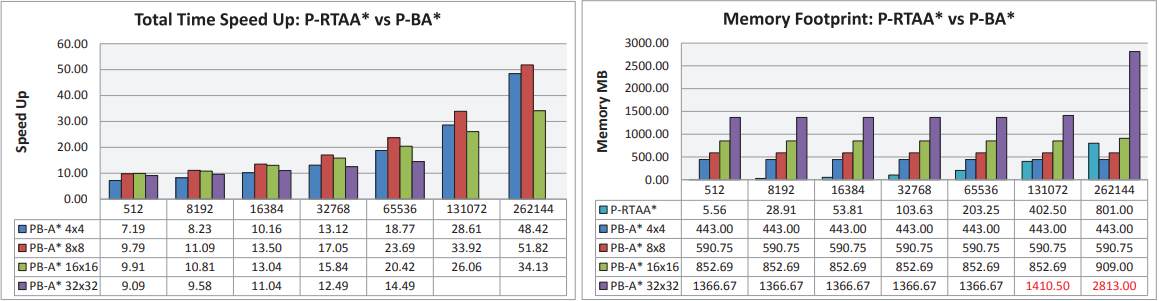image-20240414212056122
(b) 1024 × 1024 地图的 GPU 总时间加速和内存占用。

图 6：与 RTAA* 的 GPU 实现（代理组大小从 512 到 262144 不等）相比，GPU 总时间加速值和内存占用量。我们还包括从 CPU 到 GPU 传输数据的时间，反之亦然。 内存占用用于边界到边界和开始到边界搜索。 请注意，在两种情况下所需的内存高于可用于计算的内存。

​ 使用尺寸为 512 × 512 和 1024 × 1024 的两个网格图以及尺寸从 512 到 262144 不等的几组代理来评估性能和内存占用，规划块的尺寸为 4 × 4、8 × 8、16 × 16 和 32 × 32. 在 P-RTAA* 中，搜索数量以及 GPU 上运行的线程数量始终等于代理数量。 相反，在 P-BA* 中，代理的数量仅决定开始到边界搜索的数量，因为边界到边界搜索取决于规划块尺寸和边界图块的数量。 例如，在 1024 × 1024 映射中，我们测试的所有规划块大小有 786432、458752、245760 和 126976 个线程。

​ 在所有配置中，起始位置是在网格地图中随机选择的，而停止图块始终是地图的中心图块。 此外，启发式值 h[s] 是离线预先计算的，并存储在与网格图一样大的矩阵中。 图 6 报告了与 P-RTAA* 相比的 GPU 总加速时间和内存占用量。 RTAA* 的 GPU 实现始终以 Lookahead = 3 执行，这是实现最佳性能的最佳值，如 [7] 中所述。 结果表明我们的方法比 P-RTAA* 更快。 每组代理的平均加速加速度在512×512地图中从5X到45X，在1024×1024地图中从9X到44X； 测量的时间值包括内存传输时间（CPU 到 GPU，反之亦然）和内核执行时间。但是，尽管我们观察到共享内存可以提高性能，但它的使用意味着测试配置之间存在一定程度的差异。 相反，P-RTTA* 在大多数情况下表现出更好的内存占用，因为与 P-RTAA* 相比，存储边界到边界步骤中生成的搜索需要更大的内存量。 然而，随着代理数量的增加，搜索数量预计将大幅增加，内存占用也会大幅增加。 请注意，一般来说，8×8 的规划块在加速和内存占用方面提供更好的性能。

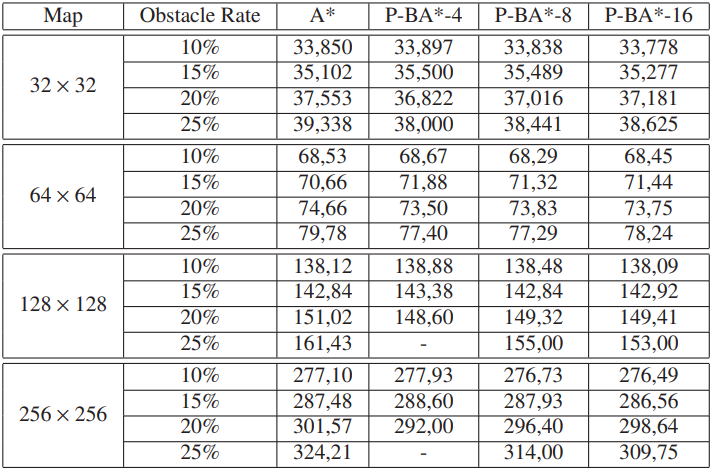
image-20240414212415573

​

表 1：A* 和 P-BA* 的平均步长。

​ 第二种类型的实验涉及通过引入规划块的方法获得的路径长度。 我们使用 32 × 32、64 × 64、128 × 128 和 256 × 256 网格地图测量平均路径长度，障碍物比例不断增加。 使用尺寸为 4×4、8×8 和 16×16 的规划块进行 1 次 A* 搜索和 3 次 P-BA* 搜索，以左上角为起始位置，右下角为目标位置。 表 1 列出了 100 次运行的平均路径长度。 对于每次运行，我们都会放置随机选择的障碍物，因此，可能会有一些地图没有从起点到目标位置的路径。 结果表明，用我们的方法检索的路径长度与用顺序 A* 计算的路径长度基本相同，并且增加规划块的大小涉及接近最优解的路径长度。

​ 这些实验表明，我们的方法找到的路径与最佳路径长度的差异并不显着。 正如性能实验所示，这种缺陷在效率方面得到了补偿。微调规划块尺寸允许用户在速度与路径最优性之间进行权衡。 例如，在实时应用中，速度是最高优先级，因此次优路径可能是可接受的。

7. Conclusion(结论)

​ 在这项工作中，我们展示了一种基于 A* 算法的并行实现，非常适合 GPU 并行架构。 通过使用它来探索每个线程的每个潜在子路径，该方法提供了一种简单而强大的方法来并行规划数千个代理的轨迹。 我们的结果表明，GPU 实现比 RTAA* 提高了 45 倍，即使在具有大量代理的场景中也可以实时使用该技术，这在视频游戏等应用中很常见。

​ 未来的工作可能会进一步探索共享记忆，特别是探索如何提高其在边境到边境步骤中的影响。 研究网格地图中出现的动态障碍物的管理也很有趣。 一旦系统识别出动态障碍物的存在，只有在发生动态障碍物的规划块中才会执行新的边界到边界和/或开始到边界步骤。 因此，所有检索到的组合多个子路径的路径应该能够快速适应地图中的变化。

​ 我们还提出了该技术的扩展，以使用核外技术来管理非常大的映射，以减少内存占用需求。 最后，我们打算通过开源许可证发布此实现。

References(参考)

  1. P. Hart, N. Nilsson, B. Raphael, A formal basis for the heuristic determination of minimum cost paths,Systems Science and Cybernetics, IEEE Transactions on 4 (2) (1968) 100 –107.
  2. S. Koenig, M. Likhachev, Real-Time Adaptive A*, in: Proceedings of the fifth international joint conference on Autonomous agents and multiagent systems, AAMAS ’06, ACM, New York, NY, USA, 2006,pp. 281–288.
  3. A. Bleiweiss, GPU accelerated pathfinding, in: Proceedings of the 23rd ACM SIGGRAPH/EUROGRAPHICS symposium on Graphics hardware, GH ’08, Eurographics Association, Aire-la-Ville, Switzerland,Switzerland, 2008, pp. 65–74.
  4. G. J. Katz, J. T. Kider, Jr, All-pairs shortest-paths for large graphs on the GPU, in: Proceedings of the 23rd ACM SIGGRAPH/EUROGRAPHICS symposium on Graphics hardware, GH ’08, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 2008, pp. 47–55.
  5. E. Stefan, S. Damian, Parallel state space search on the GPU, in: International Symposium on Combinatorial Search (SoCS), 2009.
  6. J. Kider, M. Henderson, M. Likhachev, A. Safonova, High-dimensional planning on the GPU, in: Robotics and Automation (ICRA), 2010 IEEE International Conference on, 2010, pp. 2515 –2522. doi:10.1109/ROBOT.2010.5509470.
  7. U. Erra, G. Caggianese, Real-time Adaptive GPU multi-agent path planning, GPU Computing Gems Jade Edition Edition, Vol. 2, Morgan Kaufmann Publishers Inc., 2011, Ch. 22, pp. 295–308.
  8. J. Nickolls, I. Buck, M. Garland, K. Skadron, Scalable parallel programming with CUDA, Queue 6 (2) (2008) 40–53.
  9. Nvdia, NVIDIA CUDA Compute Unified Device Architecture - Programming guide.